Expectation Maximization and Gaussian Mixture Models

1. Introduction

---

This is my attempt to go through the math completely of Gaussian Mixture Models. I also discuss why the alternating of the $E$ and $M$ steps converges to a good solution, pathological solutions, and some matrix algebra.

2. Problem Setup

---

Let’s begin by specifying our data and task. Given \(\{x_n\}_{n = 1}^N = X \in \mathbb{R}^{n \times d}\), each data point \(x_n\) has an associated latent indicator variable $z_n \in \mathbb{R}^K$ where $z_n$ is a one-hot vector, i.e. $z_{nk} = 1 \implies x \in C_k$ where $C_k$ is the $k$’th component.

We’ll additionally assume each point $x_n$ was generated by a single Gaussian so $C_k$ could be thought of as all the points generated by the $k$’th multivariate Gaussian.

Our task is to figure out $p(z_{nk} \mid x_n)$ - this is the probability that a point $x_n$ belongs to the $k$’th MVG.

For a concrete motivating example, say we’re tracking several herds of animals and we’ve tracked various sightings of said animals and recorded their locations. The herds are distinct but occasionally animals from different herds will be sighted in the same place. Our job is to figure out, given a sighting at a specific location, which herd that animal belongs to: in other words, we want $p(z_{nk} \mid x)$ or the posterior distribution. We have the constraint that $\sum_{k = 1}^K p(z_{nk}) = 1$.

Let’s define $\pi_k = p(z_{k})$ - this is the prior distribution of the different $k$ components independent on the location. So if we know one of the herds is much larger than the other, we’d give it a larger mixture coefficient (modeling our data as a mixture of Gaussians).

So we can write:

\[\begin{aligned} p(x_n) &= \sum_{k = 1}^K p(x_n, z_{nk}) \\ &= \sum_{K = 1}^K p(x_n \mid z_{nk}) p(z_{nk}) \end{aligned}\]

The probability of a single point $x_n$ given $z_{nk} = 1$ means that we are conditioning on the possibility that $x_n$ is generated from the $k$’th multivariate Gaussian. So,

\[\begin{aligned} p(x_n) = \sum_{k = 1}^K \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \pi_k \end{aligned}\]

Next, let’s also establish some other basic representations.

\[p(z_n) = \prod_{k = 1}^K \pi_k^{z_{nk}}\]

We’re taking advantage that $z_{nk}$ is only $1$ for one $k$ - so this reduces to $p(z_n) = \pi_k$ for some $k$. We’ll do the same for expressing the conditional:

\[p(x_n \mid z_n) = \prod_{k = 1}^K \mathcal{N}(x_n \mid \mu_k, \Sigma_k)^{z_{nk}}\]

3. MLE

---

Now, let’s try MLE on the dataset. We define our parameters:

\[\Theta = \{\mu, \Sigma, \pi\}\]

as the means, covariance matrices, and mixing coefficients of the different components.

\[\begin{aligned} L(\Theta \mid X) &= p(X \mid \Theta) \\ &= \prod_{n = 1}^N p(x_n \mid \Theta) \\ &= \prod_{n = 1}^N \sum_{k = 1}^K \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \pi_k \\ l(\Theta \mid X) &= \sum_{n = 1}^N \ln \left \{ \sum_{k = 1}^K \pi_k \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right \} \label{eq:hard} \end{aligned}\]

The term is hard to optimize due to the log of sums. So MLE is computationally intractable. Fortunately, there’s still a way to solve this problem.

4. Expectation Maximization

4.1 E-step

---

The algorithm used to solve this problem is called Expectation Maximization. Pretend for a second we knew the ground truth and had access to the complete dataset, ${X, Z}$. At this point we compute an expected value. So we can write:

\[\begin{aligned} L(\Theta \mid X, Z) &= p(X, Z \mid \Theta) \\ &= p(X \mid Z, \Theta) p(Z \mid \Theta) \\ &= \prod_{n = 1}^N p(x_n \mid z_n, \Theta) \prod_{n = 1}^N p(z_n \mid \Theta) \\ &= \prod_{n = 1}^N p(x_n \mid z_n, \Theta) p(z_n \mid \Theta) \\ &= \prod_{n = 1}^N \prod_{k = 1}^K \left \{ \pi_k \mathcal{N}(\mu_k, \Sigma_k) \right \}^{z_{nk}} \\ l(\Theta \mid X, Z) &= \sum_{n = 1}^N \sum_{k = 1}^K z_{nk} \left [ \ln \pi_k + \ln \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right ] \end{aligned}\]

The log-likelihood of the complete dataset has a much nicer form than the log-likelihood of the incomplete dataset. However, latent variables are well... latent. If we had access to component ground truths, we wouldn’t need to do density estimation. So instead, we can optimize the expected value of the log-likelihood of the complete dataset under the posterior distribution $p(z \mid x)$.

Just by using Bayes Rule we can write:

\[\gamma(z_{nk}) = p(z_{nk} \mid x_n) = \frac{p(z_{nk}, x_n)}{p(x_n)} = \frac{\pi_k \mathcal{N}(x_n \mid \mu_k, \Sigma_k)} {\sum_{k = 1}^K \pi_k \mathcal{N}(x_n \mid \mu_k, \Sigma_k)}\]

If $z_{nk}$ is an indicator variable, then $\gamma(z_{nk})$ is the probability that $z_{nk} = 1$. The probability that an indicator variable is $1$ is its expected value, i.e. $\mathbb{E}[z_{nk}] = \gamma(z_{nk})$.

So we have:

\[\mathbb{E}_{z \mid x}[ \ln p(X, Z \mid \theta)] = \mathbb{E} \left [ \sum_{n = 1}^N \sum_{k = 1}^K z_{nk} \left [ \ln \pi_k + \ln \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right ] \right ]\]

By linearity and since $\pi_k$ and the normal don’t depend on $z$, we have:

\[\mathbb{E}_{z \mid x}[ \ln p(X, Z \mid \theta)] = \sum_{n = 1}^N \sum_{k = 1}^K \mathbb{E}[z_{nk}] \left [ \ln \pi_k + \ln \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right ]\] \[\mathbb{E}_{z \mid x}[ \ln p(X, Z \mid \theta)] = \sum_{n = 1}^N \sum_{k = 1}^K \gamma(z_{nk}) \left [ \ln \pi_k + \ln \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right ]\]

4.2 M-Step

---

At this point, we maximize that value w.r.t $\Theta$. Specifically, we have:

\[\Theta^\text{new} = \mathop{\mathrm{arg\,max}}_{\Theta} \ \mathbb{E}_{z \mid x}[ \ln p(X, Z \mid \theta)]\]

Recall our parameters are the mixture coefficients, covariance matrices, and means. So we’ll do the following derivations.

4.2.1 Means

---

First, let’s compute the derivative w.r.t. the means. We’ll just ignore the sums for now since it practically doesn’t matter (derivative is linear) and the term $\gamma$.

\[\frac{\partial E}{\partial \mu_k} = \frac{\partial}{\partial \mu_k} \left \{ \ln (\pi_k) + \ln \mathcal{N}(x_n \mid \mu_k, \Sigma_k) \right \}\]

Let’s expand the logarithms:

\[= \frac{\partial}{\partial \mu_k} \left \{ \ln (\pi_k) - \frac{1}{2} (x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) - \frac{d}{2} \ln(2 \pi) - \frac{1}{2} \ln \det(\Sigma_k) \right \}\]

The innermost sum goes away since we derive w.r.t. one specific mean. So we have:

\[\frac{\partial E}{\partial \mu_k} = - \frac{1}{2} \sum_{n = 1}^N \gamma(z_{nk}) \frac{\partial}{\partial \mu_k} (x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k)\]

The derivative of $x^T A x$ w.r.t. $x$ is $(A + A^T) x$ so we have (since $\Sigma^{-1}$ is symmetric as $\Sigma$ is a symmetric matrix).

\[0 = \sum_{n = 1}^N \gamma(z_{nk}) \Sigma_k^{-1} (x_n - \mu_k)\]

Left-multiply both sides by $\Sigma$ and we get:

\[0 = \sum_{n = 1}^N \gamma(z_{nk}) x_n - \sum_{n = 1}^N \gamma(z_{nk}) \mu_k\]

Define $N_k = \sum_{n = 1}^N \gamma(z_{nk})$. So we have:

\[\mu_k^* = \frac{1}{N_k} \sum_{n = 1}^N \gamma(z_{nk}) x_n\]

So the MLE of the $k$’th mean is the posterior probability of belonging to the $k$th component multiplied by the value data point normalized by the effective number of points assigned to cluster $k$.

4.2.2 Covariances

---

Next, we’ll do the same for the covariance matrix. First, $\frac{\partial \det(X)}{\partial X} = \det(X) (X^{-1})^T$ so $\frac{\partial \log \det(X)}{\partial X} = (X^{-1})^T$ (49 in Matrix Cookbook).

\[= \frac{\partial}{\partial \Sigma_k} \left \{ \ln (\pi_k) - \frac{1}{2} (x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) - \frac{d}{2} \ln(2 \pi) - \frac{1}{2} \ln \det(\Sigma_k) \right \}\]

The $\pi$ terms go away. So we have:

\[= - \frac{1}{2} \Sigma_k^{-1} - \frac{1}{2} \frac{\partial}{\partial \Sigma_k} (x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k)\]

By (61) in the Matrix Cookbook, we have:

\[\frac{\partial}{\partial X} a^T X^{-1} a = - X^{-T} aa^T X^{-T}\] \[\frac{\partial}{\partial \Sigma_k} (x_n - \mu_k)^T \Sigma_k^{-1} (x_n - \mu_k) = - \Sigma_k ^{-1} (x_n - \mu_k) (x_n - \mu_k)^T \Sigma_k^{-1}\]

So we have (since again, the inner sum disappears):

\[\frac{\partial E}{\partial \Sigma_k} = - \frac{1}{2} \sum_{n = 1}^N \gamma(z_{nk}) \left \{ \Sigma_k^{-1} - \Sigma_k^{-1} (x_n - \mu_k) (x_n - \mu_k)^T \Sigma_k^{-1} \right \}\]

We can write this:

\[\begin{aligned} 0 &= - \frac{1}{2} \Sigma_k^{-1} \left [ N_k I - \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T \Sigma_k^{-1} \right ] \\ &= N_k I - \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T \Sigma_k^{-1} \\ N_k I &= \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T \Sigma_k^{-1} \\ N_k \Sigma_k &= \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T \\ \Sigma_k^* &= \frac{1}{N_K} \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T \end{aligned}\]

So the MLE for the covariance matrix of the $k$’th compoonent is like a weighted covariance matrix (weighted by the posterior mixing components) normalized by the number of data points belonging to the $k$’th cluster.

4.2.3. Mixing Coefficients

---

Finding the MLEs of the mixing coefficients involves a Lagrange multiplier since the coefficients sum to $1$ (the others had this to but it went to $0$ during optimization).

So we optimize $E + \lambda (\sum_{k = 1}^K \pi_k - 1)$. We derive w.r.t the mixture coefficients.

\[0 = \frac{\partial E'}{\partial \pi_k} = \sum_{n = 1}^N \frac{\gamma(z_{nk})}{\pi_k} - \lambda\] \[\lambda \pi_k = \sum_{n = 1}^N \gamma(z_{nk})\]

Now, let’s sum over $k$ (mixing coefficients sum to $1$. So we have:

\[\lambda = \sum_{k = 1}^K \sum_{n = 1}^N \gamma(z_{nk}) = N\]

So we have:

\[\pi_k^* = \frac{N_k}{N}\]

The mixing coefficient for the $k$’th multivariate Gaussian is the average responsibility for the whole dataset - number of points explained over total number of points.

So in short, our MLEs are:

\[\pi_k^* = \frac{N_k}{N}\] \[\Sigma_k^* = \frac{1}{N_K} \sum_{n = 1}^N \gamma(z_{nk}) (x_n - \mu_k) (x_n - \mu_k)^T\] \[\mu_k^* = \frac{1}{N_k} \sum_{n = 1}^N \gamma(z_{nk}) x_n\]

4.2.4 Some Code

Next, we have some code written up.

def E_step(X, pi_ks, means, covs):
    k = means.shape[0]
    Gamma = np.zeros((X.shape[0], k))
    X_probs = np.zeros((X.shape[0]))

    for i in range(X.shape[0]):
        X_probs[i] = np.sum(pi_ks[j] * compute_mvg_density(mu=means[j], Sigma=covs[j], x=X[i], batch=False) for j in range(k))
    
    for i in range(X.shape[0]):
        for j in range(k):
            Gamma[i, j] = pi_ks[j] * compute_mvg_density(mu=means[j], Sigma=covs[j], x=X[i], batch=False) / X_probs[i]
    
    return Gamma


def M_step(X, pi_ks, means, covs, Gamma):
    N = X.shape[0]
    k = means.shape[0]

    for j in range(k):
        N_k = np.sum(Gamma[:, j]) # N_k = sum_n gamma_nk
        pi_ks[j] = N_k / N        # pi_k = N_k / N

        # mu_k = (sum_n gamma_nk * x_n) / N_k
        means[j] = np.sum(Gamma[n, j] * X[n] for n in range(N)) / N_k 

        # sigma_k = (sum_n gamma_nk * (x_n - mu_k)(x_n - mu_k).T) / N_k
        covs[j] = np.sum(Gamma[n, j] * np.outer(X[n] - means[j], X[n] - means[j]) for n in range(N)) / N_k


def fit_gmm(X, k, steps):
"""
Prints neg log likelihood at each step
"""
    covs = np.zeros((k, 2, 2))
    for i in range(k):
        covs[i] = make_cov_matrix(np.array([1, 1]))

    mean_point = np.average(X, axis=0)
    rands = np.random.randn(k, 2)
    means = mean_point + rands * 0.1

    pi_ks = np.random.rand(k)

    for i in range(steps):
        Gamma = E_step(X, pi_ks, means, covs)
        M_step(X, pi_ks, means, covs, Gamma)

    
    return Gamma, pi_ks, means, covs

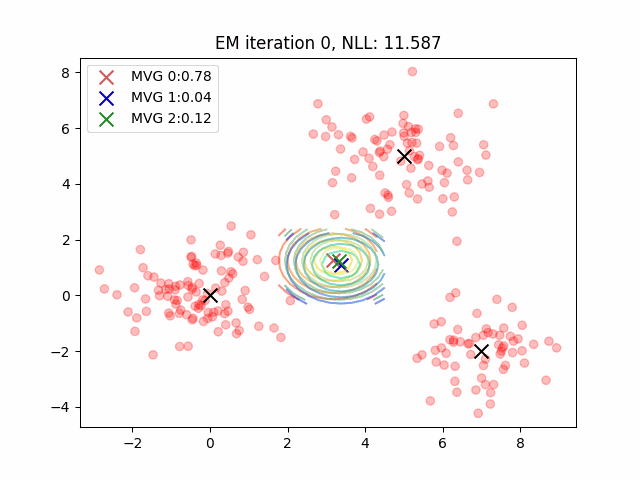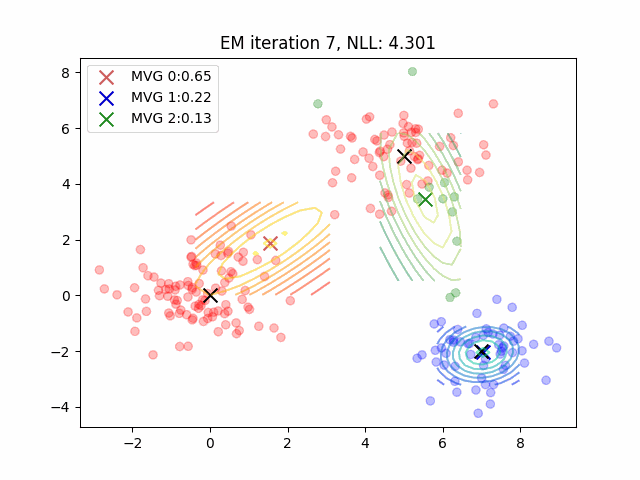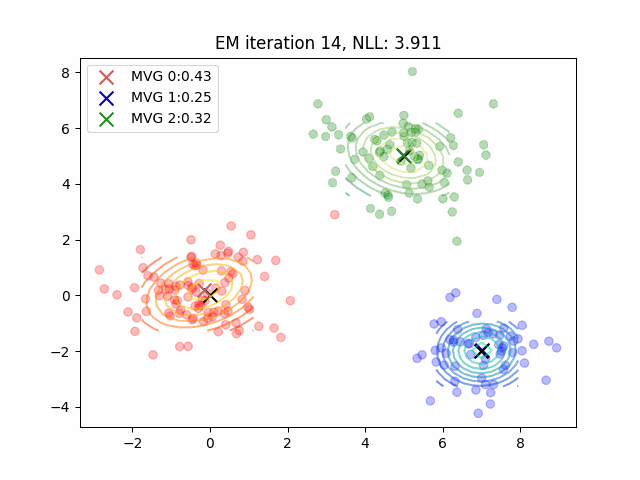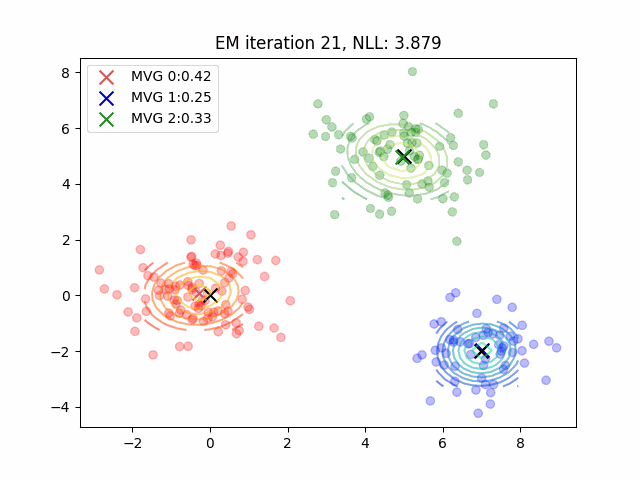
Currently, my code for fitting GMMs is maybe 4x slower than sklearn? But they both yield the same results which is pretty cool. In practice, the E-step means computing posterior probabilities while the M-step is a parameter update. There’s some more plotting code which was tough to figure out - it can all be found here. You can also use the negative log-likelihood as a proxy for how well your clustering algorithm fits the data. However, be cautious as likelihood is not necessarily a good proxy for dimensionality reduction tasks or mixture modeling for clustering tasks.

5. Generalized EM

---

We present the EM algorithm below:

1. Choose initial $\Theta^\text{old}$.

2. E step. Evaluate $p(Z \mid X, \Theta^\text{old})$.

3. M step. Evaluate $\Theta^\text{new} = \mathop{\mathrm{arg\,max}}_{\Theta} Q(\Theta, \Theta^\text{old})$.

4. Check for log likelihood or parameter value convergence. Otherwise, $\Theta^\text{old} \leftarrow \Theta^\text{new}$ and return to step $2$.

EM is a much more general algorithm than just fitting mixture models - it finds ML or MAP parameter estimates when the model depends on latent variables and optimizing the complete log-likelihood is easier than optimizing the log likelihood.

5.1. Intuition

---

We’ve done a lot of math but it’s not exactly clear at this point why alternating between the E and M step produces a better estimate of the parameters and posterior probabilities. The E-step is about computing probabilistic cluster assignments. In $k$-means, this is saying which points belong to which clusters - the assignment step. The M-step is about updating $\Theta$, cluster properties. The idea behing EM is to find a lower bound on likelihood $L(\Theta \mid X)$. Maximizing this lower bound leads to higher likelihood values. Starting with $\Theta^\text{old}$ we construct the surrogate lower bound $Q(\Theta, \Theta^\text{old})$. Then, we find $\Theta^\text{new} = \mathop{\mathrm{arg\,max}}_{\theta} Q(\Theta, \Theta^\text{old})$. We repeat, constructing another surrogate.

Recall our log-likelihood quantity:

\[l(\Theta \mid X) = \sum_{n = 1}^N \log \sum_{k = 1}^K p(x_n, z_{nk} \mid \Theta)\]

We can re-write this:

\[= \sum_{n = 1}^N \log \sum_{k = 1}^K p(z_{nk} \mid x_n, \Theta) \frac{p(x_n, z_{nk})}{p(z_{nk} \mid x_n, \Theta}\]

The weighted average $\sum_{k = 1}^K p(z_{nk} \mid x_n)$ is an expectation over $z_{nk} \mid x_n$. So we can write:

\[l(\Theta \mid X) = \sum_{n = 1}^N \log \mathbb{E}_{z \mid x} \left [ \frac{p(x_n, z_{nk} \mid \Theta)}{p(z_{nk} \mid x_n, \Theta)} \right ]\]

We can take advantage of Jensen’s Inequality. For linear functions, we have $\mathbb{E}[f(x)] = f(\mathbb{E}[x])$. For convex functions which curve upwards and thus have more large values, we have that the average output is larger than the output of the largest input or $f(\mathbb{E}[x]) \leq \mathbb{E}[f(x)]$.

The logarithm is a concave function (in which case, by the same reasoning the inequality is reversed) - so set $f(x) = - \log x$. Then, $\log (\mathbb{E}X) \geq \mathbb{E} \log X$. So we have:

\[l(\Theta \mid X) \geq \sum_{n = 1}^N \mathbb{E}_{z \mid x} \ln \frac{p(x_n, z_{nk} \mid \Theta)}{p(z_{nk} \mid x_n, \Theta)}\] \[= \sum_{n = 1}^N \mathbb{E}_{z \mid x} \ln p(x_n, z_{nk}) - \ln p(z_{nk} \mid x_n, \Theta)\]

The term within the sum becomes:

\[= \mathbb{E}_{z \mid x} [\ln p(x_n, z_{nk} \mid \Theta)] - \mathbb{E}_{z \mid x} [\log p(z_{nk} \mid x_n, \Theta)]\]

This is the complete log-likelihood plus the entropy of the conditional distribution $z \mid x$. It can actually be shown that if we multiply by one using $p(z \mid x, \Theta)$, the lower-bound is tight.

Let’s call the expected value of the complete log-likelihood $Q(\Theta \mid \Theta^\text{old})$ and the entropy $H(\Theta \mid \Theta^{\text{old}})$. Recall that entropy is non-negative (you cannot have negative surprisal). In some sense, we are almost done. We compute a lower-bound on the likelihood of the data given our existing parameters (E-step) and then maximize that lower-bound (M-step). However, how do we know that maximizing our lower-bound will improve our likelihood? Gibb’s Inequality states:

\[H(\Theta \mid \Theta^\text{old}) \geq H(\Theta^\text{old} \mid \Theta^\text{old})\]

Cross-entropy is always greater than entropy. So we can write:

\[\begin{aligned} \ln p(x \mid \Theta) - \ln p(x \mid \Theta^\text{old}) &= Q(\Theta \mid \Theta^\text{old}) - Q(\Theta^\text{old} \mid \Theta^\text{old}) + H(\Theta \mid \Theta^\text{old}) - H(\Theta^\text{old} \mid \Theta^\text{old}) \\ &\geq Q(\Theta \mid \Theta^\text{old}) - Q(\Theta^\text{old} \mid \Theta^\text{old}) \end{aligned}\]

In other words, if we maximize $Q(\Theta^\text{old} \mid \Theta^\text{old})$, then we maximize the log-likelihood of the data point by the same amount.

5.2 Pathological Solution

---

We don’t actually want to maximize the likelihood of the data with a Gaussian Mixture Model. If we shape one MVG as a point-mass on a single data point and let another MVG give non-zero mass to the other data points, then the likelihood will essentially go to infinity. To see, this observe:

\[L(X \mid \Theta) = \prod_{n = 1}^N \frac{\pi_1}{\sqrt{2 \pi \sigma_1^2}} \exp \left \{ - \frac{1}{2 \sigma_1^2} (x_n - \mu_1)^2 \right \} + \frac{\pi_2}{\sqrt{2 \pi \sigma_2^2}} \exp \left \{ - \frac{1}{2 \sigma_2^2 } (x_n - \mu_2)^2 \right \}\]

By setting $\mu_1 = x_n$ and letting $\sigma_1^2 \to 0$, we can get infinite likelihood for a single data point $x_n$. The exponential term has a small numerator and a small denominator but is positive. Meanwhile, the mixing coefficient becomes really large because the denominator goes to $0$. The other MVG gives non-zero mass to other points so we have the product of a very large number with a bunch of other non-zero numbers.

This is an example of MLE overfitting - it suggests that MLE is not a good objective function at all for this sort of problem and we need to introduce some sort of prior or constraint on our parameters.

6. Conclusion

---

This view of EM leads to the generalized paradigm of variational inference (minimizing KL-divergence between some parameterized proposal dist. and the true distribution through maximizing lower bound on marginal likelihood). The opposite view leads to expectation propagation. All very interesting stuff. Recently, I’ve been reading up on information theory. I also aim for my next post to be on diffusion models and various other generative models. Also at some point I want to code up a diffusion model.

7. References

---

Gregory Gundersen, Expectation–Maximization, 10 Nov. 2019. https://gregorygundersen.com/ blog/2019/11/10/em

Bishop, Christopher M. Pattern Recognition and Machine Learning. New York :Springer, 2006. Chapter 9

Rudin, Cynthia. Intuition for the Algorithms of Machine Learning, Self-pub, eBook, 2020 Chapter 11. https://users.cs.duke.edu/ cdr42/teaching.html

Petersen, K. B., & Pedersen, M. S. (2006). The Matrix Cookbook. Technical University of Denmark. http://www2.imm.dtu.dk/pubdb/p.php?3274